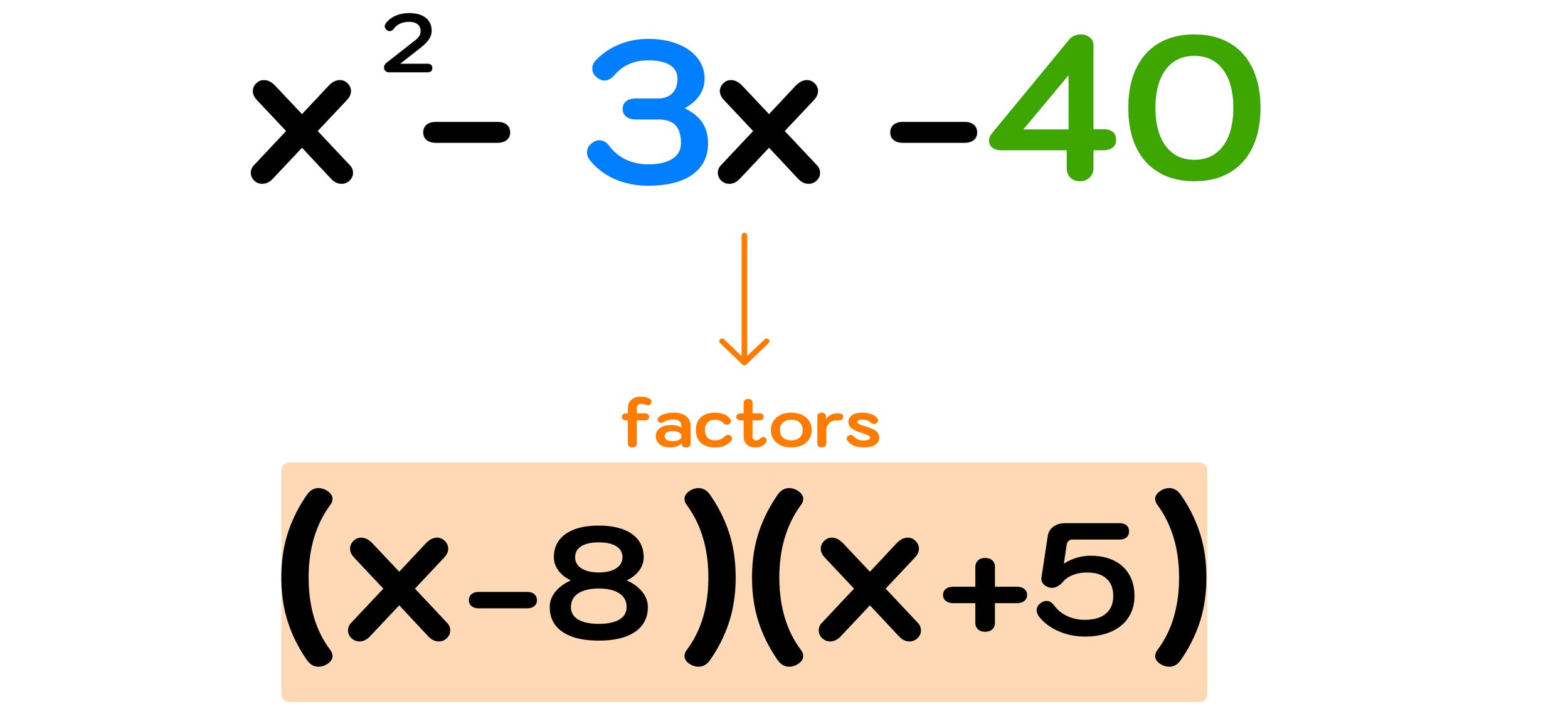Ever found yourself staring at a complex algebraic expression, feeling utterly lost? Factoring, the seemingly mysterious process of breaking down expressions, is, in reality, a foundational skill that unlocks the secrets of algebra, making the complex simple and the unsolvable solvable.
Factoring, at its heart, is the reverse of the multiplication process. Instead of multiplying terms together to get a single expression, you're dissecting an expression into its constituent parts, or factors. This skill is not just a classroom exercise; it's a vital tool that permeates various aspects of mathematics, particularly when simplifying complex equations and tackling more advanced concepts like calculus.
The journey into factoring begins with understanding the fundamental concepts. Students often encounter factoring for the first time in the 6th grade, building upon their existing knowledge of expressions and equations. As they progress through algebra and beyond, the ability to factor expressions evolves, becoming more sophisticated and crucial for problem-solving.
- Games Like Summertime Saga Top Picks For Fans In 2024 Beyond
- Diddy Party What It Is Why Theyre Still Talked About
Consider factoring as the art of reverse engineering mathematical expressions. When we factor, were essentially un-multiplying, taking a product and breaking it down into its components, like taking apart a complex machine to understand its inner workings. This skill is far more than an academic exercise; it's a foundational tool that simplifies equations, reveals the roots of polynomials, and streamlines problem-solving in various fields, from physics to economics.
The core idea of factoring revolves around rewriting mathematical expressions as products of their factors. This process is essential for simplifying expressions and solving quadratic equations. In essence, you're breaking down complex expressions into simpler, more manageable parts.
Factoring isn't merely about finding an answer; its about gaining a deeper understanding of mathematical relationships. Think of it like this: when you factor an expression, you are essentially revealing the hidden structure, or the "DNA" of the equation. This is often the critical first step for untangling a problem. You are, in essence, deconstructing it into its most basic building blocks.
- Kevin Leonardos Nair Video Butt Hair Removal Goes Viral
- Chris Noth Meet His Sons Orion Keats Family Life
One common approach to factoring involves identifying the greatest common factor (GCF) within an expression. The GCF is the largest factor shared by all the terms in the expression. By extracting the GCF, you simplify the expression and often reveal a more manageable form. For example, in the expression $3x^2 + 6x$, the GCF is $3x$. Factoring out $3x$ gives us $3x(x + 2)$, a much clearer and more useful form. The technique of factoring is also used in solving quadratic equations.
Here is a summary of various factoring methods:
- Factoring Numbers: A basic step, involves finding the prime factors of a number. For example, the prime factors of 12 are 2, 2, and 3.
- Factoring Out the Greatest Common Factor (GCF): Identifying the largest factor common to all terms in an expression and extracting it.
- Factoring by Grouping: Used for expressions with four or more terms, where terms are grouped, and GCF is factored from each group to reveal a common binomial factor.
- Factoring Trinomials: Converting a trinomial (a polynomial with three terms) into a product of two binomials. Examples include factoring trinomials where the leading coefficient is 1 ($a=1$) and where it is not ($a \neq 1$).
- Difference of Squares: Factoring expressions in the form of $a^2 - b^2$ into $(a+b)(a-b)$.
Prime numbers, the building blocks of all integers, are central to factoring. A prime number is a whole number greater than 1 that has only two factors: 1 and itself. Examples include 2, 3, 5, 7, and so on. Understanding prime numbers helps in completely factoring numbers into their prime factors, a fundamental step in many factoring problems.
In algebra, factoring often leads to equations in a form that can be easily solved. The ability to factor allows us to rewrite equations as products of expressions that can be set equal to zero. When the product of two or more expressions equals zero, at least one of those expressions must equal zero, which allows you to find the roots, or solutions, of the original equation.
Factoring is an essential skill in algebra for simplifying expressions, simplifying fractions, and solving equations. It is an important process in algebra which is used to simplify expressions, simplify fractions, and solve equations. When we simplify the given expression into its factors then this process is called factoring. Factoring algebra is the process of factoring algebraic terms. To understand it in a simple way, it is like splitting an expression into a multiplication of simpler expressions.
Factoring offers a toolkit of strategies for simplifying complex expressions, revealing their underlying structure, and ultimately, solving for unknown variables. By learning to recognize patterns and apply the correct methods, you gain a powerful advantage in your mathematical endeavors.
Let's look at some examples.
Example 1: Factoring out the Greatest Common Factor (GCF)
Consider the expression: $12x^2 + 18x$.
The GCF of $12x^2$ and $18x$ is $6x$.
Factoring out $6x$, we get: $6x(2x + 3)$.
Example 2: Factoring by Grouping
Consider the expression: $2x^3 + x^2 + 6x + 3$.
Group the first two terms and the last two terms: $(2x^3 + x^2) + (6x + 3)$.
Factor out the GCF from each group: $x^2(2x + 1) + 3(2x + 1)$.
Factor out the common binomial factor $(2x + 1)$: $(2x + 1)(x^2 + 3)$.
Example 3: Factoring a Trinomial
Consider the expression: $x^2 + 5x + 6$.
Find two numbers that multiply to 6 and add up to 5. These numbers are 2 and 3.
Factor the trinomial: $(x + 2)(x + 3)$.
Example 4: Difference of Squares
Consider the expression: $x^2 - 9$.
Recognize this as a difference of squares ($x^2 - 3^2$).
Factor it: $(x + 3)(x - 3)$.
The importance of factoring extends beyond just solving problems. It develops an appreciation for the structure of mathematical relationships. By mastering factoring, you're not just learning a set of techniques; youre developing a way of thinking that promotes clarity, efficiency, and a deeper understanding of the world of mathematics.
In mathematics, a factor is a number or algebraic expression that divides another number or expression evenly, that is, with no remainder. For example, 3 and 6 are factors of 12 because 12 3 = 4 exactly and 12 6 = 2 exactly.
The factoring calculator transforms complex expressions into a product of simpler factors. Factoring trinomials is converting an algebraic expression from a trinomial expression to a binomial expression.
One of the factoring techniques that you are going to learn in this module is factoring by greatest common monomial factor (gcmf). The math journey around factoring methods starts with what a student already knows, and goes on to creatively crafting a fresh concept in the young minds. Done in a way that not only it is relatable and easy to grasp, but also will stay with them forever.
Factoring is a fundamental skill, not only in the field of mathematics but also in many other areas. It is used to simplify the given expression into simpler terms.
What is prime factorization?
Prime factorization is the method that allows every integer that is greater than 1 to be expressed as the product of prime integers.
This knowledge serves as a stepping stone for tackling more complex mathematical challenges. Finding what to multiply to get an expression. For example: 2y+6 = 2(y+3), so the factors of 2y+6 are: 2 and (y+3) (called factorizing in British English.)
To understand it in a simple way, it is like splitting an expression into a multiplication of simpler expressions known as factoring expression example: 2y + 6 = 2(y + 3).
Factoring is often taught with examples, exercises and the use of identities to aid in mastering the skills.
You can think of a prime factor as the building block of a number, and a common factor as a bridge connecting two numbers together. Concepts such as factors, factoring, and prime factorization have been discussed and have been used in many instances in your previous math classes.
With practice and perseverance, anyone can master factoring and unlock a new level of mathematical understanding.
A common method of factoring numbers is to completely factor the number into positive prime factors. A prime number is a number whose only positive factors are 1 and itself. For example, 2, 3, 5, and 7 are all examples of prime numbers. Examples of numbers that arent prime are 4, 6, and 12 to pick a few. To factor in algebra, i usually start by identifying the greatest common factor of the terms within an expression. For example, if i come across an expression like $3x^2 + 6x$, i can pull out a $3x$ to get $3x(x + 2)$.
In algebra, one method for solving equations is to factor them when possible. This is because factoring gives us an equation in the form of a product of expressions that we can set equal to 0. If the product of two (or more) expressions is equal to 0, as is the case when we factor polynomials, at least one of the expressions must equal 0.
In elementary algebra, factoring a polynomial reduces the problem of finding its roots to finding the roots of the factors. Polynomials with coefficients in the integers or in a field possess the unique factorization property, a version of the fundamental theorem of arithmetic with prime numbers replaced by irreducible polynomials.
Factoring Numbers - Start Here
Factoring numbers is an essential skill that is required in mathematics. It involves breaking down a number into a product of its factors. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. The prime factorization of 12 is 2 x 2 x 3, which is its breakdown into prime numbers.
Finding a Greatest Common Factor (GCF)
The GCF is the biggest number that goes into two or more numbers without any remainders. To find the GCF:
- List the factors of each number.
- Identify the common factors.
- Choose the greatest one.
Factoring a GCF from an Expression
This involves identifying the GCF of the terms in an expression and then rewriting the expression by factoring out that GCF. For example, in the expression 6x + 9, the GCF is 3. Factoring out 3 gives 3(2x + 3).
Factoring a Difference Between Two
This method is used when an expression is in the form of a2 - b2. The formula for factoring a difference of squares is a2 - b2 = (a + b)(a - b). For example, x2 - 4 can be factored as (x + 2)(x - 2).
The next few lessons explain how to factor numbers, expressions, and equations.
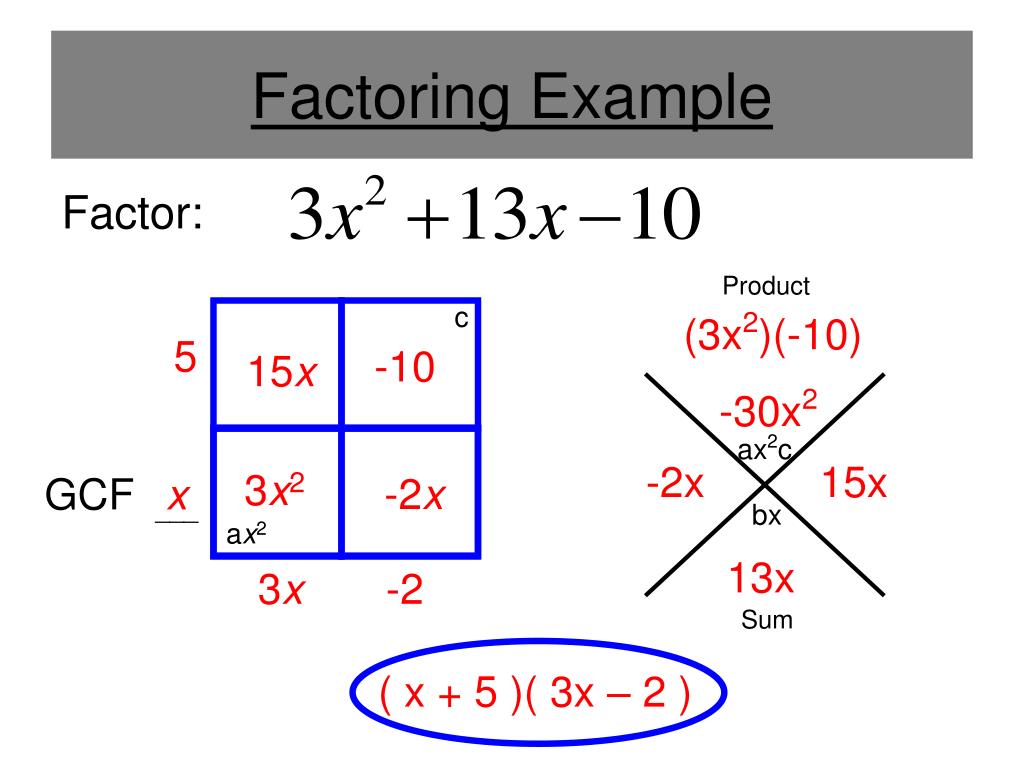
Factor, in mathematics, a number or algebraic expression that divides another number or expression evenlyi.e., with no remainder. For example, 3 and 6 are factors of 12 because 12 3 = 4 exactly and 12 6 = 2 exactly. The other factors of 12 are 1, 2, 4, and 12. Factoring is the process of decomposing or splitting any given polynomial into a product of two or more polynomials. Factoring trinomials is converting an algebraic expression from a trinomial expression to a binomial expression. A trinomial is a polynomial with three terms with the general expression as ax 2 + bx + c, where a and b are coefficients and c is a constant.
Here is table with information related to factoring
| Category | Description |
|---|---|
| Definition | Rewriting mathematical expressions as products of their factors. |
| Purpose | Simplifying expressions and solving equations. |
| Basic Concepts | Finding common factors, using identities, and checking answers. |
| Methods |
|
| Applications |
|
| Example | Factoring $x^2 + 5x + 6$ into $(x + 2)(x + 3)$ |
| Key Terms | Factor, Greatest Common Factor (GCF), Prime Number, Trinomial, Binomial, Roots |
| Level | Generally introduced in 6th grade, expanded throughout algebra and beyond. |
| Relevance | Essential skill in algebra, simplifying expressions, and solving equations by revealing their roots. |
| Skills developed | Pattern recognition, algebraic manipulation, and problem-solving. |
This is not a procedure used commonly in everyday life. A number or expression's factor is the value that divides it equally without producing leftovers. 2 and 3 are factors of 6. Factoring refers to the separation of a formula, number or matrix into products.
Where to Learn More
For more in-depth explanations and examples, consider exploring resources like Khan Academy, Math is Fun, or your textbooks algebra section. The ability to factor, an essential skill in algebra for simplifying expressions and solving equations by revealing their roots, is built over time.
- Anime Game Illustrations Discover Explore Now
- Graphing Linear Functions Methods Examples Amp Solutions Learn Now