Can the complexities of the world be elegantly visualized with the simplicity of a line? Graphing linear equations allows us to visually represent relationships between variables, offering a powerful tool for understanding and predicting behaviors across various fields.
At its core, graphing linear equations is the process of depicting linear equations with one or two variables on a coordinate plane. A linear equation, defined by its degree of one, signifies that the highest power or exponent of the variable is invariably 1. This fundamental characteristic ensures that the graphical representation of such an equation will always be a straight line. This straight line is not merely a geometric construct; it is a window into the relationship between variables, allowing us to explore trends, predict outcomes, and analyze the underlying mathematical dynamics.
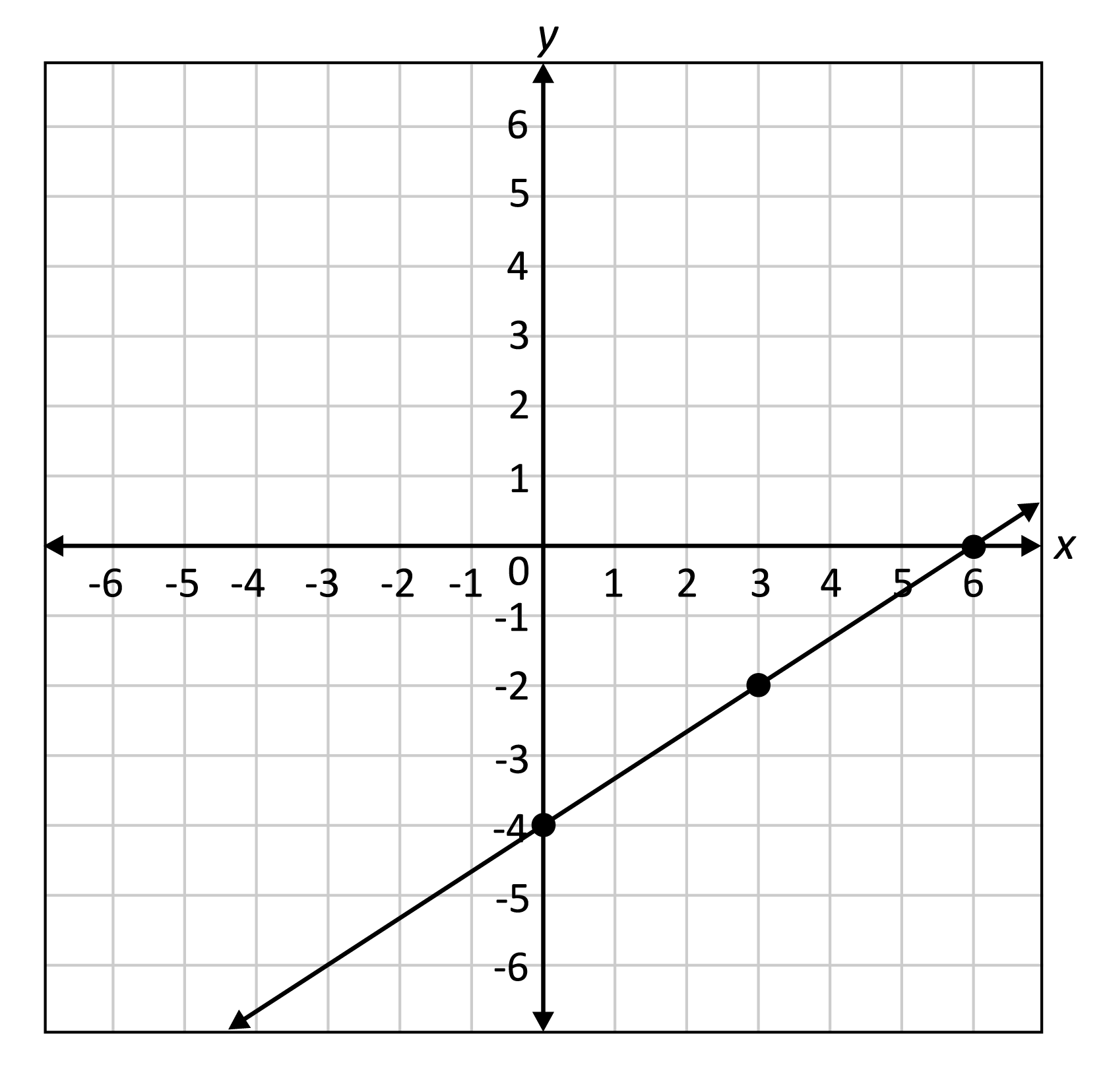
There are fundamentally three basic methods of graphing linear functions. The first involves plotting points and drawing a line through them. To accomplish this, input values are chosen, the function is evaluated at these inputs, and the corresponding output values are calculated. This provides the necessary coordinates to plot the points on the graph, after which a straight line is drawn through them. The second method involves graphing linear functions using the x and y intercepts, this method is helpful for easily visualize where the line crosses each axis. The third method, which builds upon the initial one, utilizes the initial value (output when x = 0) and the rate of change (slope) of the function. This approach provides a more streamlined method of graph creation by focusing on key characteristics.
- Alyx Star Facts Bio Age Net Worth More Uncovered
- Daryle Singletarys Death What We Know Cause Of Death Updates
This section will delve into the key features and methodologies employed in working with linear graphs, providing illustrative examples complete with detailed solutions to enhance understanding. We will also analyze the equation y = mx + c, where 'm' represents the slope of the line and 'c' represents the y-intercept, guiding us to understand how these components shape the line's position and direction on the coordinate plane. We will further explore the advantages of graphing, including its capacity to show relationships, compare different graphs, and pinpoint solutions to the equations.
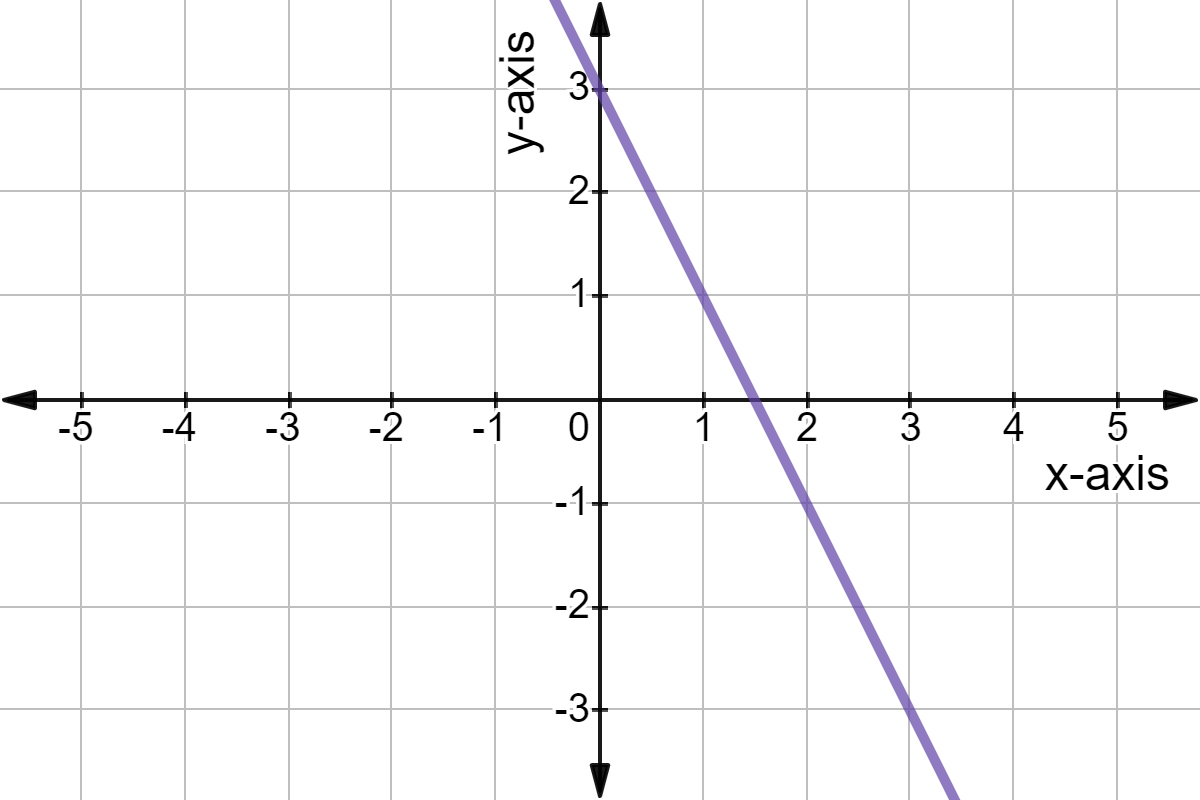
The graph of a linear function is, predictably, a straight line. In addition, the graph may exhibit a downward slant, indicating a negative slope, a feature often expected from the negative constant rate of change in the equation for the function. The ability to interpret the equation y = mx + b, where 'm' is the slope and 'b' is the y-intercept, as defining a linear function is fundamental to understanding its graphical representation.
By graphing two functions, we can more easily compare their characteristics. For example, we can analyze the functions slopes, intercepts, and any other relevant features, providing a clear view of how each function behaves.
- Coquette Aesthetic Wallpapers Download Discover
- Lela Sohna Leaks What You Need To Know The Latest Updates
The practical applications of linear equations are vast and varied. In economics, they are used to model supply and demand curves, allowing businesses to analyze market trends and make informed decisions. In physics, they are used to represent the relationship between distance, velocity, and time. In finance, they can be employed to predict future stock prices or analyze investment strategies.
Graphing linear equations also allows us to identify the points of a function and determine its initial value. The initial value, also known as the y-intercept, is the point at which the line intersects the y-axis. Understanding the initial value is crucial because it indicates the starting point of the relationship, or the value of y when x is zero. The slope, on the other hand, gives us information about the rate of change of the function. The slope of a line describes both the direction and steepness of the line. The slope can be positive (upward slant), negative (downward slant), zero (horizontal line), or undefined (vertical line). These elements work in tandem to offer a detailed overview of the linear functions nature and behavior.
The ability to graph linear equations is enhanced by interactive graphs and exercises, which allow for a more dynamic learning experience. The use of these interactive tools helps solidify conceptual understanding and encourages exploration of the function's properties. Furthermore, by matching linear functions with their graphs, or by writing the equation of a linear function from its graph, one can deepen their comprehension of the link between the equation and its visual representation.
Graphing equations without a calculator, a process that can seem daunting to some, is in fact, straightforward. By following a few steps, it becomes possible to accurately draw a linear equation. These steps include identifying the slope and y-intercept, plotting the y-intercept, using the slope to find another point, and then drawing a straight line through these points.
The following table provides the key characteristics of graphing linear equations.
| Aspect | Description |
|---|---|
| Definition | The process of representing linear equations on a coordinate plane. |
| Purpose | To visualize relationships between variables, predict values, and analyze trends. |
| Key Components | Slope (m), y-intercept (b). Equation form: y = mx + b. |
| Graph Type | Straight line. |
| Methods | Plotting points, using x and y intercepts, using initial value and rate of change (slope). |
| Applications | Economics (supply/demand), physics (motion), finance (investments). |
| Slope Interpretation | Positive slope (upward), negative slope (downward), zero slope (horizontal), undefined slope (vertical). |
| Benefits | Show relationships, compare graphs, find solutions to equations. |
Consider the example of a rectangle with its area given by the function a = s2, where s represents the side length. Because its graph contains points like (1,1), (2,4), and (3,9), which do not form a straight line, this function is not linear. Understanding this distinction is crucial when working with different types of functions.
An escalator, designed to move passengers between floors, could also be examined through the lens of linear functions. The angle of the escalator, the distance it travels, and the time it takes to transport passengers are all components that can be described using linear equations. By analyzing these elements, one can optimize the escalator's design for efficiency and passenger safety.
Graphing two functions allows us to easily compare their characteristics, we can analyze their slopes, intercepts, and any other relevant features. This comparison allows us to quickly identify the differences between the two functions.
The process of graphing linear equations encompasses various strategies. One is by plotting points, requiring at least two points and drawing a line. Another involves utilizing the initial value (output when x = 0) and the rate of change (slope). Furthermore, the ability to solve systems of equations involving two or more linear equations is another key application of graphing. The graphs of these equations will intersect at a single point if they are not parallel. Two parallel lines can also intersect if they are coincident, which means they are the same line and they intersect at every point.
The techniques of translating, reflecting, stretching, and shrinking graphs of linear functions allow us to study the transformations within the family of functions. In this setting, a family of functions is a group of functions with similar characteristics, and the most basic is defined as the parent function.
The graph of the linear equation is a set of points in the coordinate plane that all are solutions to the equation.
Some calculators, such as Symbolab, offer the functionality to draw graphs, assisting in the visualization of equations.
Graphing linear equations is a fundamental skill that has far-reaching implications in both theoretical and applied mathematics. By understanding how to graph these equations, one can unlock insights into the world of mathematics and apply them to real-world scenarios.
From the perspective of a well-informed writer, the process of graphing linear equations reveals itself as a powerful, yet accessible, method of exploring mathematical relationships. Its ability to transform complex concepts into simple, elegant lines makes it an essential tool for students, educators, and professionals in various fields.
- Brad Pitts Last Leg Career Whats Next Unveiling His Future
- Understanding Using Greater Than Or Equal To In Math