Does the seemingly abstract concept of "mathematical power" hold a tangible influence on our daily lives? The profound truth is that mathematical power shapes not only our understanding of numbers but also our very cognitive processes, impacting how we learn, solve problems, and navigate the world.
Often, the story of a single classroom offers a lens through which to understand broader, more universal truths. This is particularly true when exploring the nature of mathematical power. While a mathematical keyboard may be limited by the constraints of unicode characters, hindering the ability to, for instance, place one symbol atop another, the underlying principles remain the same: Mathematics, at its core, is a language of precision and power. It's a language that opens doors to understanding the world around us, from the most basic arithmetic to the complex theories that govern the universe.
Consider the impact of exponentiation, the core of "mathematical power." This operation, expressed as 'an', where 'a' is the base and 'n' is the exponent, signifies repeated multiplication. It's the engine behind growth, decay, and the elegant patterns found in nature. Mastering exponentiation is therefore essential for applications in mathematics, science, and engineering. The math.pow() method in Java, for example, is a testament to this, offering a computational tool widely used in various computational fields.
- Sean Kyle Swayze Bio Family Career Feud With Lisa Niemi
- Middle Finger History From Ancient Rome To Flipping The Bird
This ability to handle and interpret exponents allows us to develop a higher level of understanding, which directly affects our abilities. Mathematical power, then, is not merely about calculations; it's a gateway to a different way of thinking.
| Feature | Description |
|---|---|
| Concept | Mathematical power, is the ability to apply mathematical concepts, procedures, facts, and tools to solve problems and explain phenomena. |
| Core Components | Exponents, Indices, Powers, Exponentiation, Rules of Exponents, Fractional Exponents, Applications, Problem Solving |
| Key Terms | Base, Exponent, Power, Index, Repeated Multiplication, Exponentiation Rule, Mathematical Operation, Zero Power Rule, Power of a Product Rule, Power of a Quotient Rule |
| Influence | Affects how a person thinks, influences the ways of processing, learning result, gaining knowledge, skills, and stance reflected in daily life. |
| Applications | Mathematics, Science, Engineering, Algorithm Problems, Financial Modeling, Data Analysis, Computer Graphics, Physics, Chemistry |
| Tools | Mathematical Keyboard, Online Calculators, Java Math.pow() |
| Examples | 53 = 5 5 5 = 125, 82 = 8 8 = 64 , x1/2, Power Rule of Exponents, etc |
The importance of mathematical power is highlighted in its application to various subjects. It serves as the bedrock for development in many areas, yet paradoxically, students often find it challenging. The ability to use a number in repeated multiplication is also very important, which we call mathematical power.
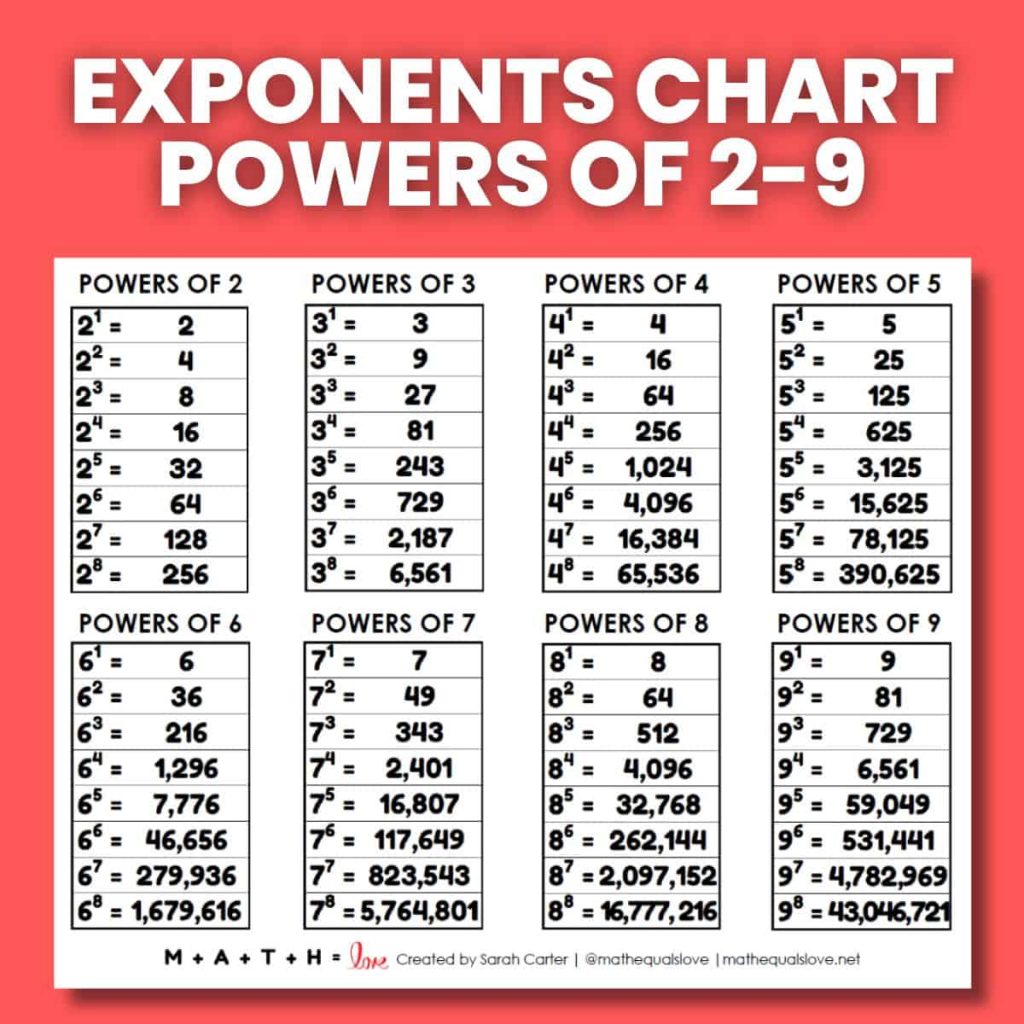
The power of a number can be represented in different ways. For example, we can express 82 as "8 to the power of 2," "8 to the second power," or simply "8 squared." Similarly, 53 is equivalent to "5 cubed." It is the repeated multiplication of a base. The terms "power" and "exponent" are often used interchangeably in mathematics to refer to the 'n' in the expression bn. This expression can be read as "b to the power of n." The term "power" can also refer to the result of the expression.
- Famous Peruvians Tula Rodrguez More Discover Their Stories
- Celine Dion Pics Swimsuits More Unseen Moments Await
Understanding mathematical power is crucial for everyone. In this context, the concept of mathematical power is not just about a set of mathematical rules. It is an important tool to help a person in various ways to gain knowledge, skill, and stance that will be reflected in their daily life. In mathematical language, a power is an exponent to which a given quantity is raised. The expression xa is therefore known as "x to the ath power."
Several rules govern the use of exponents. For example, the power of a power rule, allows us to define fractional exponents. It tells us that 91/2 = (32)1/2 = 3(21/2) = 31 = 3. Taking a number to the power of 1/2 effectively "undoes" squaring a number. Using the fractional exponents rule, this fractional power converts to a radical. Also, to divide exponents that share the same base, you retain the base and subtract the power of the denominator from the power of the numerator. Likewise, if terms in an expression have the same power but different bases, you divide the bases and raise the result to the power. And if the exponents have coefficients attached to their bases, divide the coefficients.
This principle is widely applicable in various fields, especially when dealing with algorithms. If you use a calculator that computes imaginary numbers, the answer will be a real number. Also, there are many examples, such as Example 6.1.7 power rule for exponents, Example 6.1.8 power of a product rule (pop) note, Example 6.1.9 power of a quotient rule, Example 6.1.10 example 6.1.11 example 6.1.12 exponent rules, and Example 6.1.13 zero power rule. Furthermore, the number written above a base in superscript, which we call the exponent or the index, represents how many times the base is repeated in multiplication (exponentiation).
Goodcalculators.com offers online mathematics power calculators to help in these computations. As stated in the literature, the mathematical power affects how a person thinks and processes information. Every student has the potential in them, but the levels of mathematical power differ among them. Mathematical power plays a vital role in solving complex mathematical problems.
The expression 53, for instance, is read as "5 to the power of 3," "5 to the 3rd," or "5 cubed." If the index is 1, the answer will be the number itself. For example, 51 = 5.
Mathematical power is a significant basic thing for each person who is going to learn mathematics. This ability to work with powers, or indices, helps you in learning other subjects.
- Goobersville Massacre Lunch Ladys Deadly Secret In 1949
- King Vons Death Autopsy What Happened In Atlanta