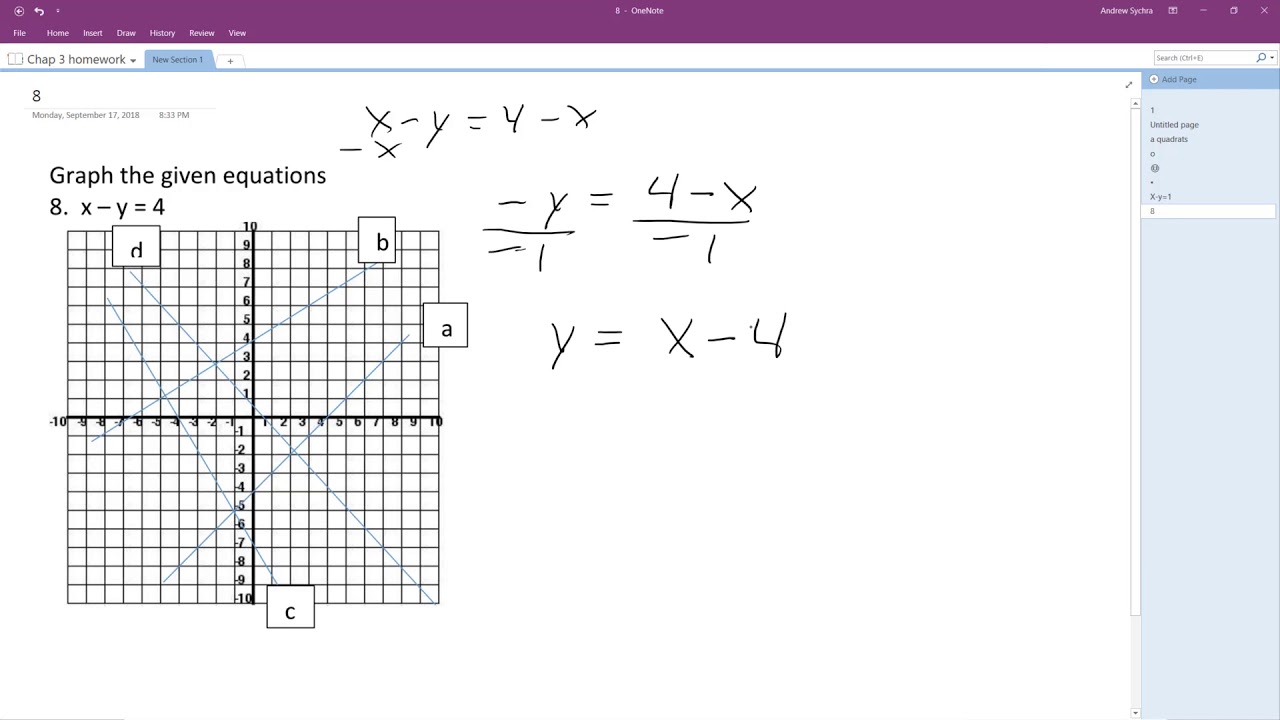
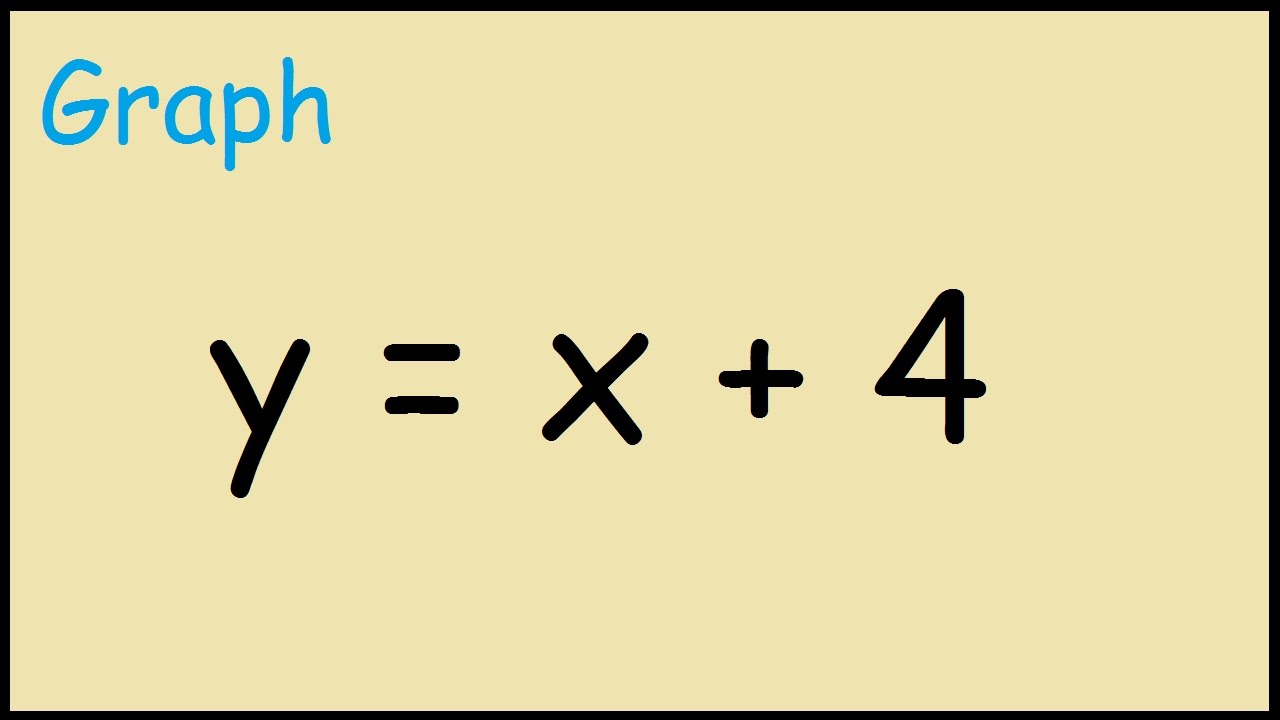Are you ready to unlock the secrets hidden within complex equations and visualize the invisible world of mathematics? Embark on a journey of discovery where numbers dance on a screen, and the abstract becomes tangible, all thanks to the power of interactive graphing calculators.
The modern graphing calculator is more than just a tool; it's a portal to understanding. It allows users to transcend the limitations of pencil and paper, offering a dynamic and interactive experience that fosters a deeper grasp of mathematical concepts. Through intuitive interfaces and powerful computational capabilities, these digital marvels transform abstract equations into visual representations, bringing clarity to the often-daunting world of functions, data, and algebraic expressions. One of the most crucial aspects of using such a powerful tool lies in understanding its basic functionalities. Learning how to input the right information is the first step to successful results.
Let's delve into the core functionalities. The first step in harnessing the power of a graphing calculator is knowing how to input your desired function. In the designated "function input section," you'll be typing in your mathematical expressions. The standard math syntax is the language you'll use here things like `x^2` for x squared, `sin(x)` for the sine function, or `log(x)` for the logarithm function. Think of it as translating your mathematical thoughts into a language the calculator understands.
- Kristi Noem News Photos And More Discover Now
- Donna Ludwig The Real Story Behind Ritchie Valens Donna Untold Tale
Once you've entered your function, you'll want to personalize the appearance of your graph. Most calculators allow you to "Select a color to represent each function on the graph." This helps in distinguishing multiple functions plotted on the same plane, making it easier to analyze their interactions and relationships. The ability to customize your graph window is paramount to seeing the specific portion you're interested in. You can use the `x min`, `x max`, `y min`, and `y max` fields to set the boundaries of your graph. This allows you to zoom in on specific areas, explore regions of interest, and effectively visualize the behavior of your functions.
The power of these calculators lies in their ability to go beyond simple plotting. They enable users to explore a vast range of mathematical concepts. These calculators are specifically designed to:
- Graph functions
- Plot points
- Visualize algebraic equations
- Add sliders (to dynamically change parameters)
- Animate graphs
- And much more.
These are not just tools for rote calculations; they are dynamic platforms for exploration. The ability to visualize these concepts fosters a more intuitive understanding. For instance, consider the impact of plotting points to understand function behavior. After plotting the points (0, 1), (1, 4), and (2, 16), you'll be able to see how the graph rises steeply, representing the rapid growth of the function. This visual confirmation reinforces the mathematical principles at play.
- Math Concepts Explained Fractions Exponents More
- Rae Dawn Chong Movies Career Life Of Tommy Chongs Daughter
Moreover, graphing calculators provide a clear illustration of how to graph a function. The process typically involves the following steps:
- First, type in your equation. An example would be `y=2x+1`. If you have a second equation, use a semicolon, like this: `y=2x+1; y=x-1`. This enables the simultaneous graphing of multiple equations, facilitating comparative analysis.
- Understanding equation manipulation, like knowing "how to add to both sides of the equation," is pivotal in simplifying and solving complex mathematical problems. The calculator can visually represent the transformations, solidifying your grasp of algebraic principles.
- Calculators frequently use a methodology where you "substitute the known values into the formula and simplify." This is a fundamental step in problem-solving.
Many offer a plethora of features to make exploration easier. GeoGebra is a prime example of an "Interactive, free online graphing calculator" which allows users to "graph functions, plot data, drag sliders, and much more!" This interactive experience is key to a deeper comprehension of concepts. Others may offer options to "Choose grid size and resolution for better control over detail and speed," and "Use the checkboxes to show or hide elements like axes and labels." These options allow users to fine-tune their visualizations, highlighting key aspects of the graph and creating a more tailored learning experience. By using these features, users can gain a high degree of control over the visual representation of their mathematical problems.
Many graphing utilities boast comprehensive capabilities. "Function grapher is a full-featured graphing utility that supports graphing up to 5 functions together." This capacity allows for multi-faceted analysis of intersecting functions. A bonus feature is the ability to save your work for future reference, "You can also save your work as a URL (website link)." This facilitates the sharing of your work, allowing you to create a portfolio of visualizations that can be easily accessed and shared.
The ability to plot functions stems from the user's capacity to learn how to input data correctly. "Usage to plot a function just type it into the function box." The variable will be `x`, therefore, always use `x` as the variable. You can even start with an introductory graph, using examples like `y = 4x` to see how functions are drawn, and observe the equation written in its functional notation `f(x) = 4x`.
To grasp the core concept, many users start by creating tables of values to plot points on the graph. For simple equations, you might begin by graphing `x = y`. In testing the validity of your results, "Next check a point not on the line." However, note that "the graph of the line contains the point (0,0), so we cannot use it as a checkpoint." This highlights the importance of selecting diverse points to validate your function accurately. The usage of graphing calculators provides an understanding of core mathematical concepts.
Furthermore, graphing calculators facilitate understanding and manipulating different types of functions. By "using the form to find the variables used to find the amplitude, period, phase shift, and vertical shift" of a trigonometric function, learners can gain an intuitive understanding of how these parameters affect the function's behavior. They can visualize the transformations and analyze the results immediately, building a deeper comprehension of complex functions.
Graphing calculators bring math to life, and allow the user to explore the world of exponential functions. With these types of functions, you are expected to encounter a horizontal asymptote. The calculators also enable users to study the equations of the horizontal asymptotes.
The interactive features of these calculators are important. For example, you may encounter the same features as the "Interactive, free online graphing calculator from geogebra", which will provide you the ability to "Graph functions, plot data, drag sliders, and much more!"
Moreover, users can also tailor their graphs by making their own configurations: "Customize your graph window using the x min, x max, y min, and y max fields."
These capabilities extend beyond pure plotting, including visualization. One of the core benefits is to explore, experiment, and understand. These tools encourage a more active and engaging approach to learning mathematics. They are not just tools for calculations; they are powerful educational platforms that allow users to manipulate equations, observe patterns, and gain a deeper, more intuitive grasp of mathematics.
The key to mastering any graphing calculator lies in the process of experimentation. Embrace the learning curve, don't be afraid to experiment with different functions and settings, and remember that the most valuable lessons often come from exploring and making mistakes. With consistent use, the tool will become a trusted companion in your mathematical journey. The more you use it, the easier it gets.
This is the sample table to show the usage:
| Feature | Description | Benefit |
|---|---|---|
| Function Input | Entering equations using standard math syntax (x^2, sin(x), log(x)) | Allows precise function definition for visualization. |
| Color Selection | Assigning colors to functions on the graph | Aids in differentiating multiple functions. |
| Axis Customization (x/y min/max) | Setting boundaries for the graph window | Focuses on specific graph regions and behaviors. |
| Plotting Points | Visualizing individual points on the graph | Clarifies function behavior by demonstrating how functions work. |
| Graphing of Equations | Plotting standard equations such as y=2x+1 | Provides a direct visualization of algebraic relationships. |
| Slider Integration | Including adjustable parameters within equations | Offers a dynamic experience for exploring function changes. |
| Asymptote Indication | Identifying horizontal asymptotes for exponential functions | Provides insights into function limits. |
| Grid and Resolution | Options for modifying the visual detail | Enhances understanding of graphs. |
| Hiding/Showing Elements | Enabling and disabling axes, labels, and grids | Supports clarity, focusing on relevant graph components. |
| URL Saving | The ability to save and share graphs | Enables the communication and reference of graphs. |
If the topic is not related to person, then we can provide the following information in tabular format:
| Tool | Description | Benefits |
|---|---|---|
| GeoGebra | Interactive, free online graphing calculator | Dynamic graphing, data plotting, slider use. |
| Function Grapher | Graphing utility supporting multiple functions | Comparative analysis and complex function exploration. |
| Online Graphing Calculators | Free online interactive calculators | Accessibility and immediate data visualization. |
| Table of Values | Method for plotting by hand | Foundation of understanding and plotting. |
| Equation Simplification | Add to both sides of the equation | Simplifies and solves mathematical problems. |
| Variable Use (x) | Use x as the standard variable | Unifies function entry and graph recognition. |
| Customization Options | Grid size, axis, labels, element modification | Greater control over visual details. |
- Ukarame Meaning Japanese Confectionery Cultural Significance
- Brattygbaby Leaks 2024 Exclusive Onlyfans Content