Exploring Linear Equations: Definitions, Forms, & Examples

Is there a hidden language governing the very fabric of our reality, a language woven from lines and relationships? Linearity, the bedrock of countless mathematical and scientific concepts, is a fundamental principle that shapes our understanding of the world, from the simplest equations to the most complex phenomena.

The exploration of "linear" concepts, while seemingly straightforward, reveals a fascinating depth, influencing fields as diverse as physics, economics, computer science, and art. At its core, the term "linear" signifies a direct, proportional relationship between variables, where a change in one quantity results in a corresponding, predictable change in another. In mathematics, the term linear functions and equations is employed to represent these concepts.

In the realm of mathematics, a linear function is typically defined as a function that includes one or two variables, excluding any exponents. Such a function, when graphed, invariably manifests as a straight line. This characteristic is essential; should the function incorporate more variables, these must remain constant or be defined as known variables to maintain the function's linear nature.

• Leslie Kotkin Unveiling The Life Story Of Cornel Wests Exwife
• Kai Razy Leaks News What You Need To Know Now

However, linear algebra provides a different but related perspective. Within this framework, a linear function is characterized by its ability to map a sum to the sum of the images of the summands. The function adheres to the principles of linearity only when it passes through the origin, or where the constant (c) is zero, according to this definition.

The foundational work on linear systems, from the perspective of axiomatization of linear algebra, can be attributed to the work of Peano, who utilized them to describe what we recognize today as vector spaces. This perspective frames linear algebra as a study of spaces characterized by linear algebraic relationships. Furthermore, the term "linear space" was initially coined by Pincherle to refer to the concept of a vector space.

A linear equation, in its essence, is an equation that graphically manifests as a straight line. When plotted on a graph, a linear equation invariably yields a straight line. The equation's simplicity allows for easy visualization and analysis of the relationship between the variables, making it a fundamental tool in mathematics.

• Haribo Sugar Free Gummy Bears Amazon Reviews Will Shock You
• Sabrina Mcgillivray Wife Of Scott Teacher Amp Family Life

A simple instance of this is the identity function, expressed as y = x. A linear term's degree is of 1. Such terms are represented as x to the first power (x 1 ), where the "1" is implied and not written since any number raised to the first power equals itself.

The relationship between two variables in a linear context is defined as follows: When one quantity undergoes a change of a particular magnitude, the other quantity consistently changes by a specific amount. This consistency is a hallmark of linearity; the rate of change of one quantity with respect to another remains constant. This is the essence of a linear relationship its predictability and constant rate of change make it a powerful tool for modeling and understanding various phenomena.

Linear equations can take on different forms, and understanding these forms is key to solving and graphing them effectively. In essence, a linear equation is an equation for a straight line characterized by variables and constants, devoid of exponents or roots. A linear equation, when graphed, always results in a straight line, representing a fundamental concept in algebra.

Linear equations can be categorized into those with one variable and those with two variables. The simplicity of linear equations makes them an ideal entry point into the world of algebra. For example, consider a linear equation representing the total cost of purchasing apples (a) at $0.50 each and bananas (b). This equation showcases how linear functions are useful in predictions. They are simple, yet powerful.

Linearity is a fundamental concept with diverse applications, but it's essential to recognize that not all relationships are linear. The world is filled with examples of non-linear relationships, adding complexity and richness to the landscape of phenomena we observe and analyze.

Numpys linear algebra module provides a versatile toolkit for implementing linear algebra operations on any numpy array. This module facilitates a wide range of functionalities, including computing the eigenvalues of matrices and performing matrix and vector operations such as dot products, inner products, outer products, etc. It also offers capabilities for matrix exponentiation and solving both linear and tensor equations, among others.

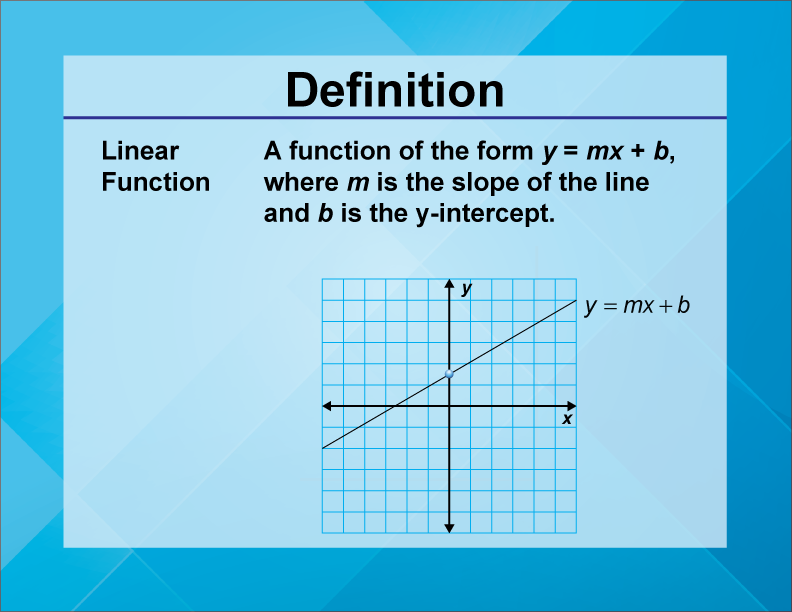
An equation of this nature is one that produces a straight line when graphed, often articulated in the y = mx+b format, where m represents the slope, and b symbolizes the y-intercept. These equations are an essential tool for representing and analyzing the relationship between variables in a visually intuitive manner. The simplicity and clarity of a linear graph make it an invaluable tool in diverse applications, from scientific modeling to economic forecasting.

A linear graph graphically represents a linear equation, providing a visual depiction of the relationship between two quantities. These graphs are characterized by straight lines, eliminating curves, dots, or other non-linear features. This approach simplifies the interpretation of data and facilitates the easy identification of trends and patterns. The ability of linear graphs to convey information concisely and clearly renders them a vital tool in diverse fields.

In mathematics, the term "linear function" encompasses two distinct but related concepts. In calculus and related fields, it refers to a function whose graph is a straight line, a polynomial function of either degree zero or one. In essence, a linear function's graph is a straight line, defined by its slope and y-intercept. This type of function includes a special kind, often useful because of its interesting and important properties.

The word "linear" inherently signifies "straight." Linear graphs serve as visual representations of linear equations, graphically illustrating the relationship between two quantities. Their design emphasizes simplicity and clarity, with straight lines depicting results, devoid of curves, dots, or bars. A "nonlinear function," conversely, describes a function whose graph deviates from a straight line, assuming curves or other non-linear forms.

For instance, consider a scenario involving an initial population of 100 fish in a pond, which doubles weekly. This is represented by the function f(x) = 100 (2) x, where x is the number of weeks, and f(x) is the fish population. Both linear and nonlinear equations generally include numbers and variables. Linear concepts inherently link to a line, where all linear equations are utilized to construct a line.

In more advanced terms, a linear equation is defined using a linear function \(f\) which is defined on a linear space, also known as a vector space (as defined in section 4.1). This advanced definition serves as the foundation for deeper explorations of linear concepts in higher mathematics and related disciplines, setting the stage for detailed discussions and in-depth analyses.